c++高精度算法

什么是高精度

有时，我们要做特别大数据的计算。多大呢？几百万位，远远超过了long long的数据范围，直接用long long肯定会溢出。这时候我们就要用高精度算法
PS：python自带高精度

所有高精度算法的基本原理

大体的思路，就是用字符数组（因为字符数组可以达到一个下标对应一个数字，达到按位处理的目的），然后转到整形数组（整型数组才能进行计算）一个下标对应一个数字，用另一个数组进行按位相加。

高精度运算

现在只写高精度加法、乘法。以后会逐渐补充

加法

思路分析

我们用数学竖式的方法来分析
别说这不是高精度，原理一样的，要不你来写个几百万位的竖式（防杠精）

这是小学数学的知识 对应位相加，有进位的加到下一位。

现在，按照刚才的思路进行模拟。仍然是134+84。但存到计算机中，再按位相加，变成了这样：

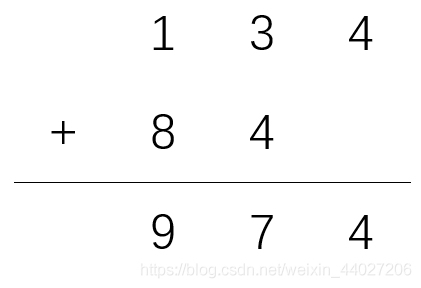
对于这种错位的情况，我们一般采取的办法是倒序存储。于是就是这样：

就是结果也是反着的。但是没关系，我们再进行倒序输出。218，没错！

代码

有了上面的说明，代码就很好懂了。

#include<iostream>
#include<cstring>
using namespace std;
int main(){
	int add1=0; //专门处理最后输出时进位的问题
	int a[1000]={},b[1000]={},c[2000]; //分别对应加数1，加数2，和
	char a1[1000],b1[1000];
	//1.输入、转换
	cin>>a1>>b1;
	//因位数可能不同，所以倒序存储要分两次完成
	for(int i=0;i<strlen(a1);i++){
		a[strlen(a1)-1-i]=a1[i]-'0'; //至于如何倒序存储，自己举例子思考，自行理解即可
	}
	for(int i=0;i<strlen(b1);i++){
		b[strlen(b1)-1-i]=b1[i]-'0';
	}
	//2.按位计算
	for(int i=0;i<max(strlen(a1),strlen(b1));i++){ //注意要用最大长度，否则计算不完
		c[i]+=a[i]+b[i]; //对应位相加。要写+=是因为进位数据以提前存好，用=会丢失数据
		c[i+1]=c[i]/10; //把进位存到下一位
		c[i]%=10; //把这一位模10，仅保留个位
		//【上边的两行顺序一定不能反，否则进位数据会丢失】
	}
	//3.输出
	//因为是加法，所以和比加数的最大长度最多只会多一位，所以只需判断一次
	if(c[max(strlen(a1),strlen(b1))]!=0){
		add1=1; //如果不是0，则说明有进位，需要多输出一次
	}
	for(int i=max(strlen(a1),strlen(b1))+add1-1;i>=0;i--){
		cout<<c[i];
	}
	return 0;
}

乘法

思路分析

有了前边加法的基础，应该很容易想到，乘法也需要倒序存储。
这里我就不多说了。

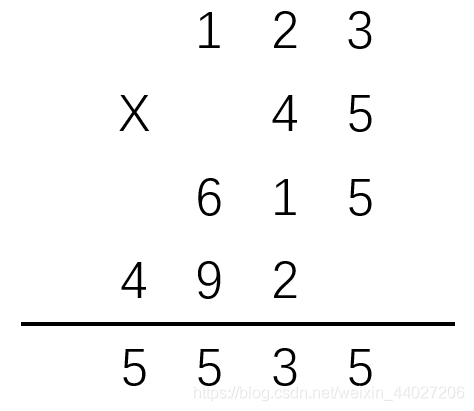
需要解释的地方如下：
1.核心计算部分
高精度乘法，实际上就是用加法模拟乘法。用乘法分配律就很好懂：

123*45=123*(40+5)=123*40+123*5

在用高精度计算时，也是一样的，只是进位处理不一样。我们用一个新的数组存储答案（这里定为c[2000]={}）==数组下标从1开始用==，c[1]+=3*5，c[1]+=2*5……，c[2]+=3*4，……
在我加粗的部分，很明显，不是从下标1开始了。原因很简单，自行列竖式理解
2.处理进位部分
这里处理进位的方法比较特殊，大体思路是把这一位除以10的结果加到下一位，并对这一位模10；下一位仍然这样，再下一位……

代码

再强调一次，此代码数组下标是从1开始用的

#include<iostream>
using namespace std;
int main(){
	string a1,b1;
	int a[2000]={},b[2000]={},c[5000]={};
	cin>>a1>>b1;
	for(int i=1;i<=a1.length();i++){ //倒序存储
		a[i]=a1[a1.length()-i]-'0';
	}
	for(int i=1;i<=b1.length();i++){
		b[i]=b1[b1.length()-i]-'0';
	}
	for(int i=1;i<=b1.length();i++){ //核心计算部分，具体解释请看思路分析
		for(int j=1;j<=a1.length();j++){
			c[i+j-1]+=a[j]*b[i];
		}
	}
	for(int i=1;i<a1.length()+b1.length();i++){ //处理进位部分，具体解释请看思路分析
		if(c[i]>9){
			c[i+1]+=c[i]/10;
			c[i]%=10;
		}
	}
	int chu=a1.length()+b1.length(); //用来处理多余的前导0
	while(c[chu]==0 && chu>1){ //如果计算结果为0，必须保留最后一位0，所以chu必须同时>1
		chu--;
	}
	for(int i=chu;i>=1;i--){ //倒序输出，没说的
		cout<<c[i];
	}
	return 0;
}